√1000以上 場合の数 組み合わせ 公式 513807-場合の数 組み合わせ 公式
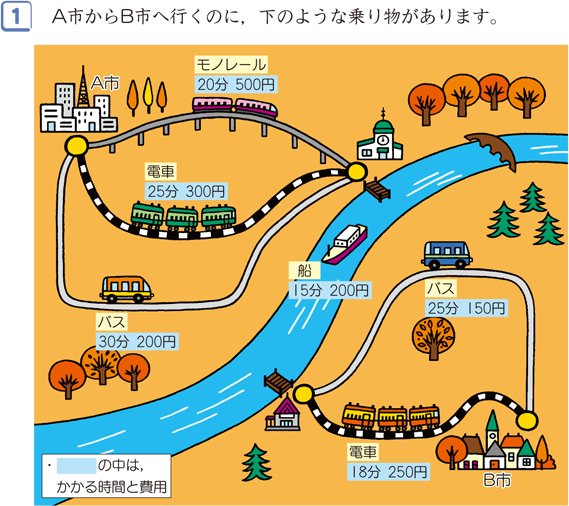
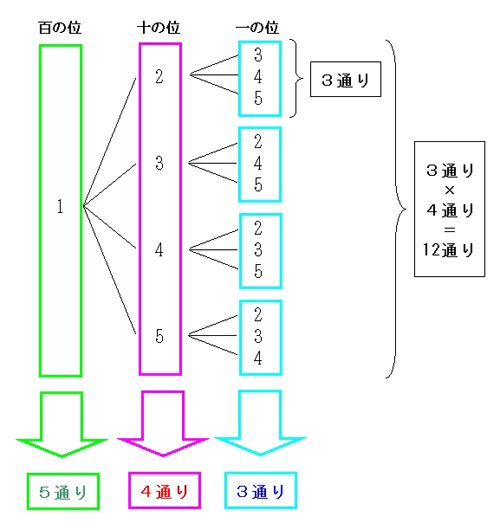
(1) 5 5 5 人の中から 2 2 2 人代表を選ぶ方法の数を求めよ。 (2) 5 5 5 人の中からリーダーと副リーダーを選ぶ方法の数を求めよ。 (3) 3 3 3 桁の正の整数で各桁の数字が 0 0 0 でなくて全て異なるものはいくつあるか。 (4) 47 47 47 都道府県から 5 5 5 つ選ぶ場合の数は
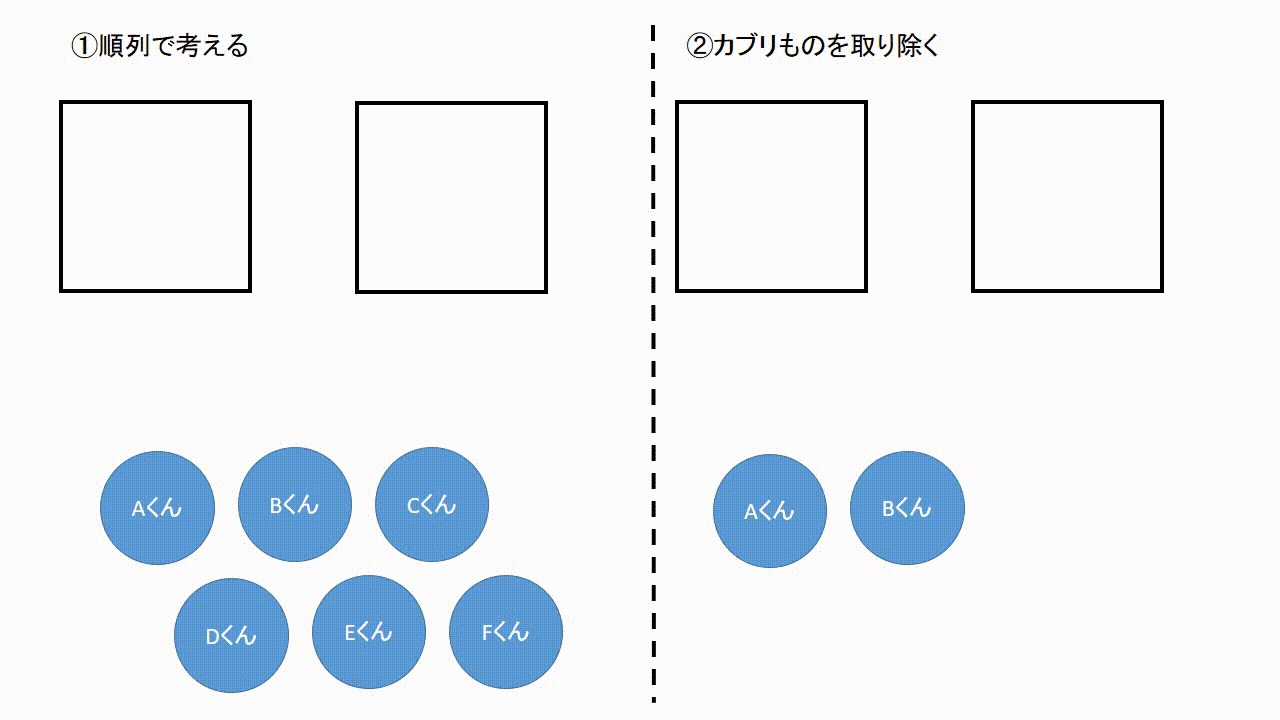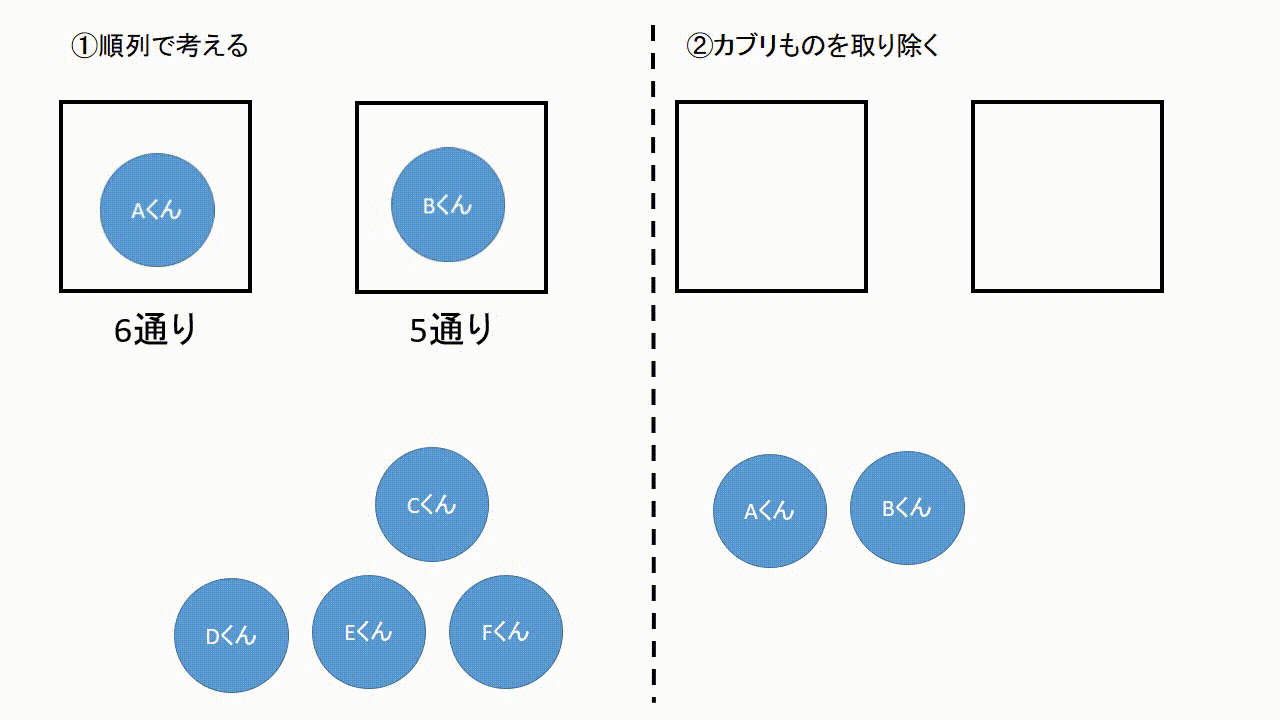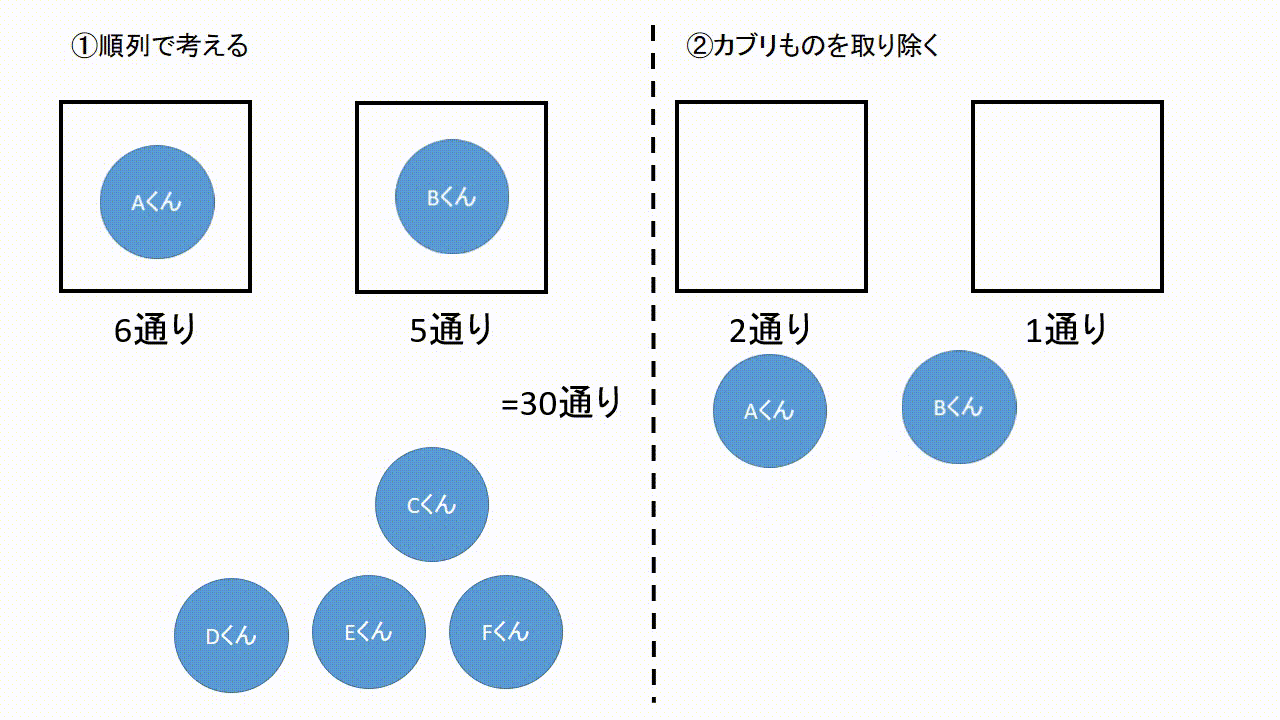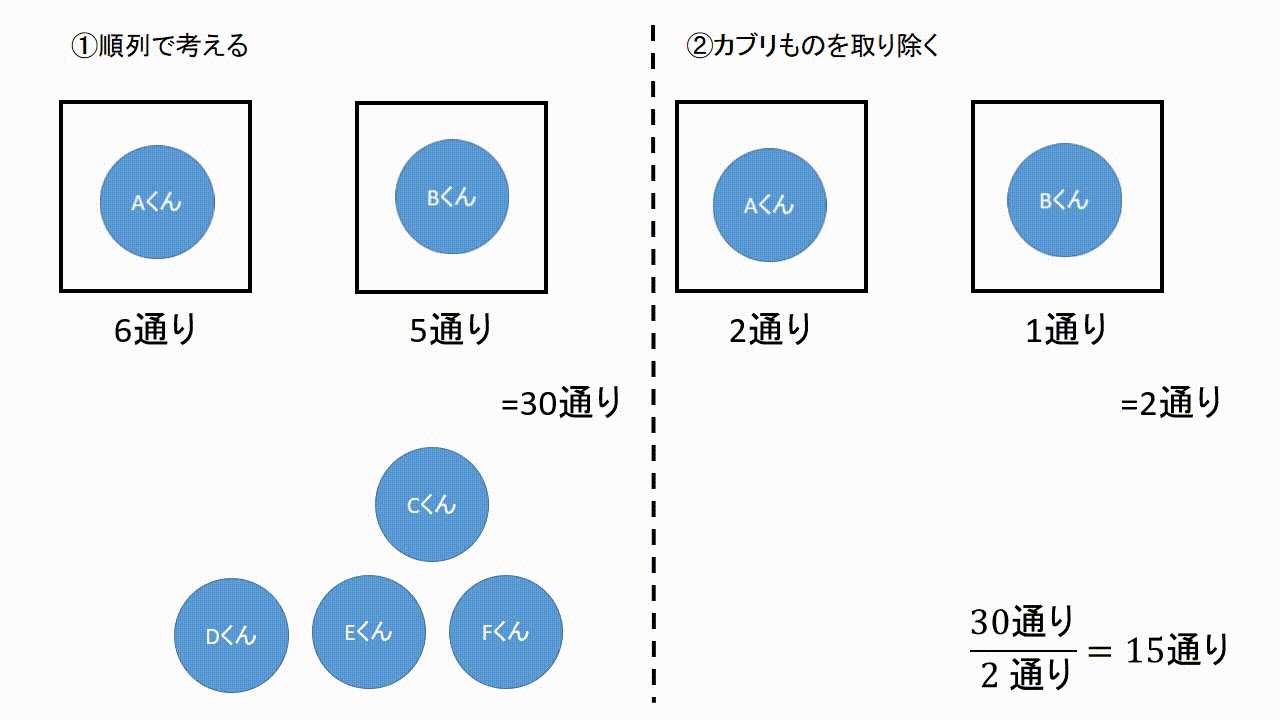
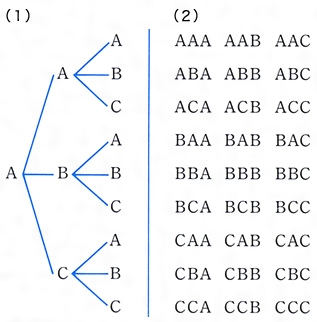
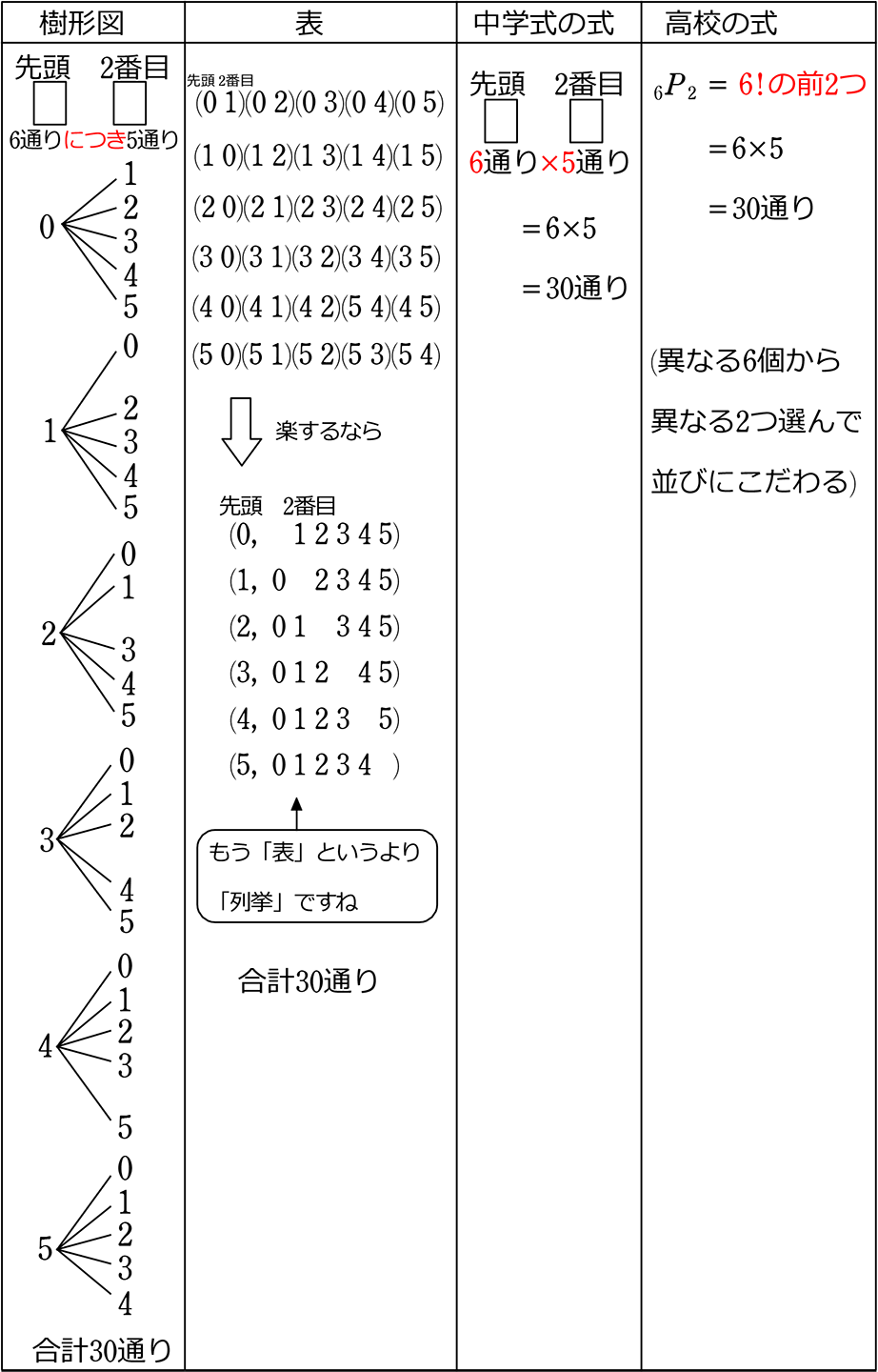
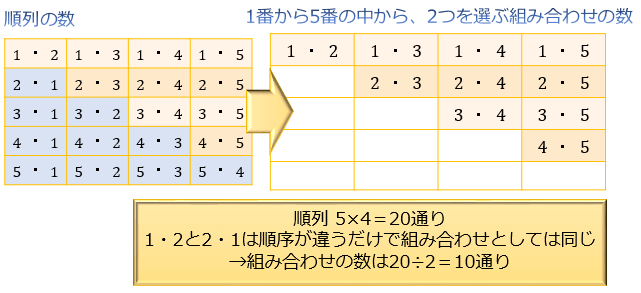
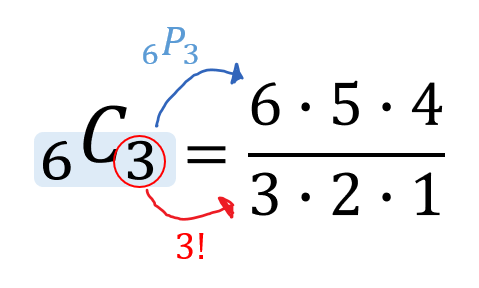
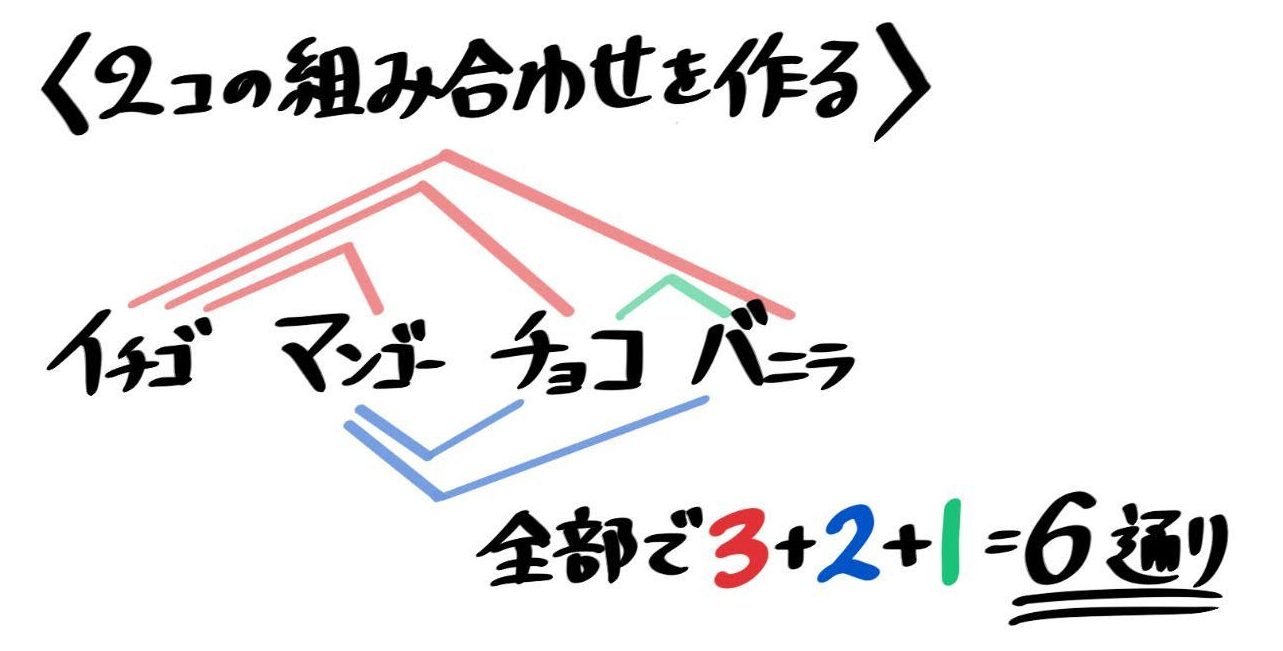
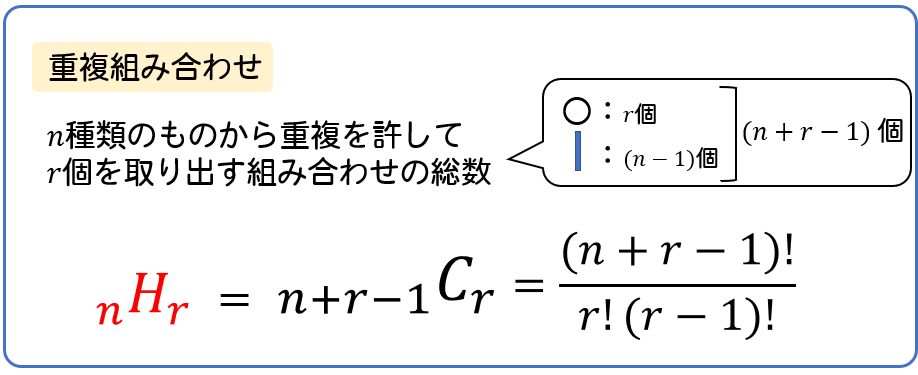
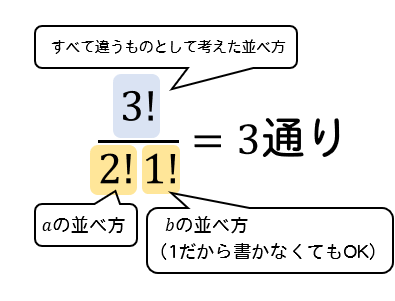
場合の数 組み合わせ 公式- ここまでの公式をまとめておきます。 どうやって作られたかも必ずみてくださいね。 Focus n 個から r 個を取り出して並べ換える場合の数は n P r = n × ( n − 1) × ⋯ ( n − r) n 個全てを並べ換える場合の数は n P n = n! これは、この組み合わせの数の公式を使う事で 5C2=5×4÷2=10通り と求めることができます。 下のように表にして考えると「並びだけが違う、組み合わせとして見たら同じものが1セットにつき 2! =2 個ずつ存在する」のが分かりやすくなります。 「1
場合の数 組み合わせ 公式のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  | |
 |  | |
 |  | |
 |  |  |
「場合の数 組み合わせ 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | |
 |  |  |
「場合の数 組み合わせ 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
 |  | |
「場合の数 組み合わせ 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
 |  |  |
「場合の数 組み合わせ 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  | |
 |  |  |
「場合の数 組み合わせ 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 | ||
 |  |  |
「場合の数 組み合わせ 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  |  |
 |  | |
 |  | |
「場合の数 組み合わせ 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  | |
 |  |  |
「場合の数 組み合わせ 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |
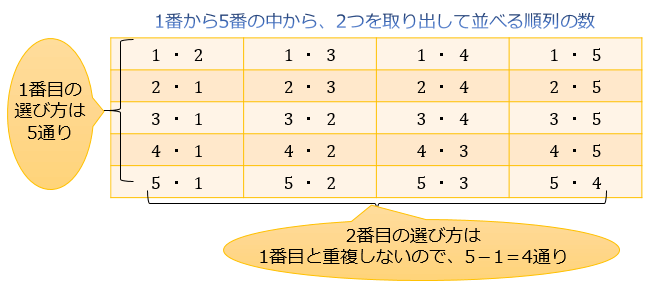
場合の数・順列組み合わせの公式 場合の数の和の法則 A、Bという2つ同時には起こらない事象がある。Aの起こり方がm通り、Bの起こり方がn通りあるとき、AまたはBの起こる場合の数は、m+n通り 場合の数の積の法則 A、Bという2つの事 順列のポイントは、 取り出す順番が関係する ということです。 つまり、「1回目にx、2回目にy、3回目にz を取り出したとき」を(x,y,z)で表すとすると、 (a,b,c)と(c,b,a)は 中身は同じですが、順番が違うため、別のものとしてカウントします。 一方で、 「組合せ(C)」では、順番を考慮しないの
Incoming Term: 場合の数 組み合わせ 公式,
コメント
コメントを投稿